[最も共有された! √] 円周の長さを求める公式 小学生 636311
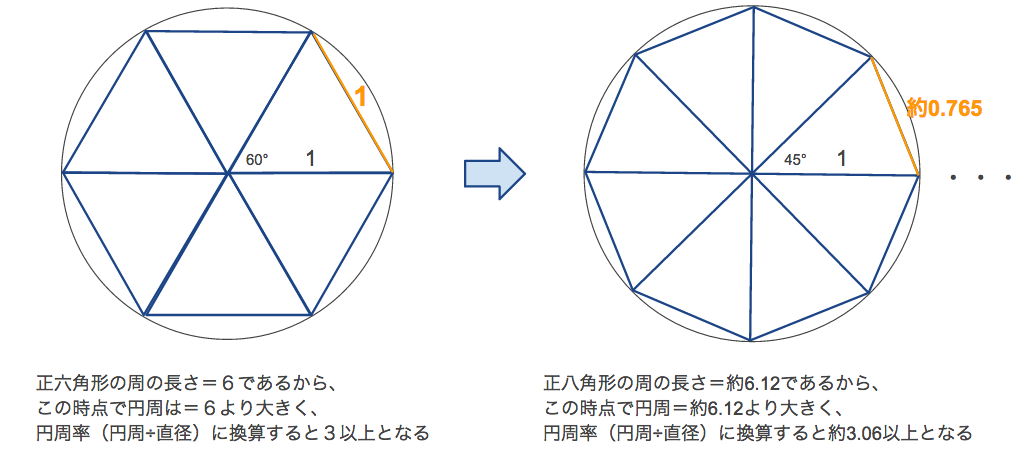
5年算数 正多角形と円周の長さ わかる教え方
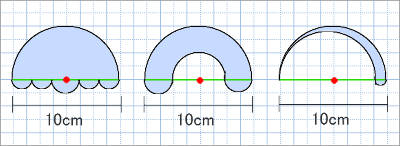
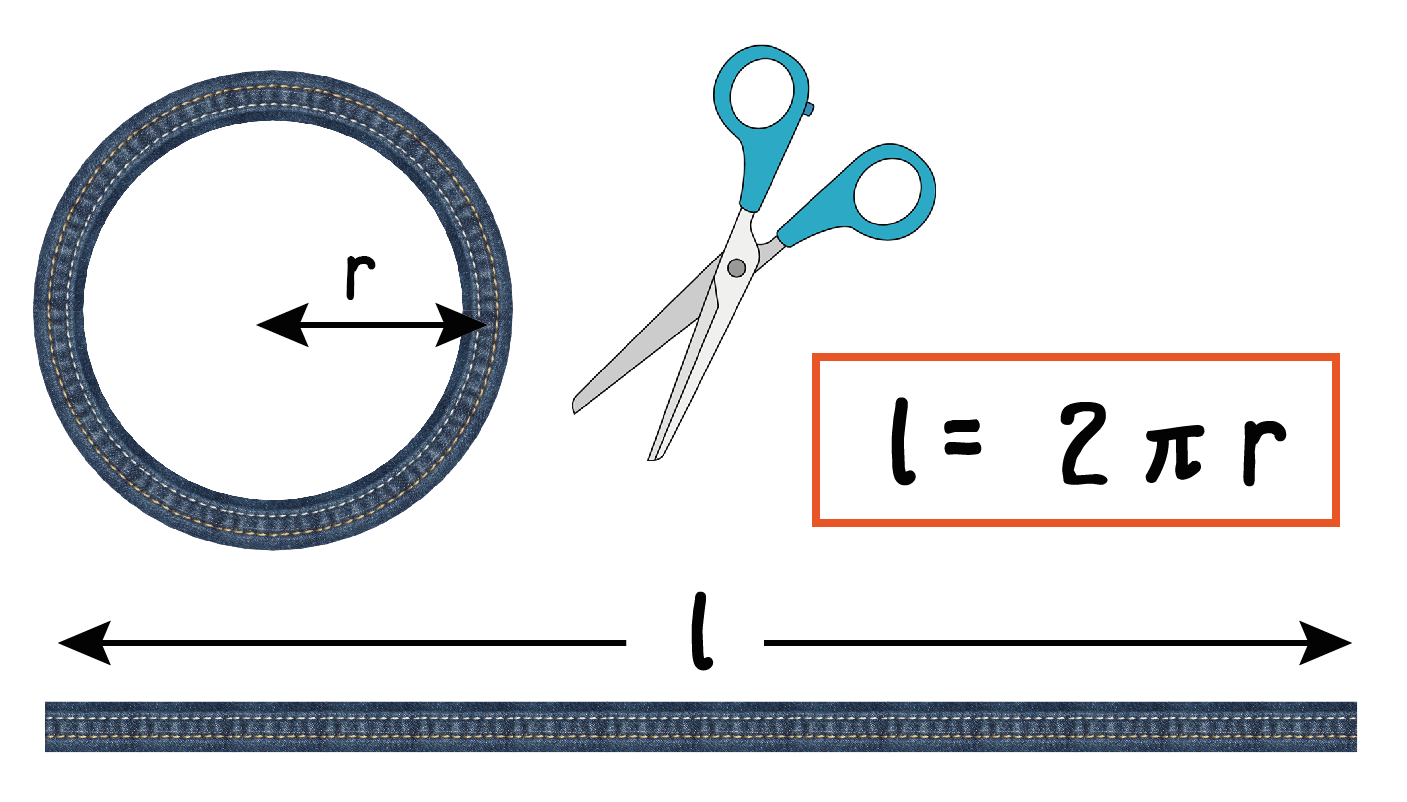
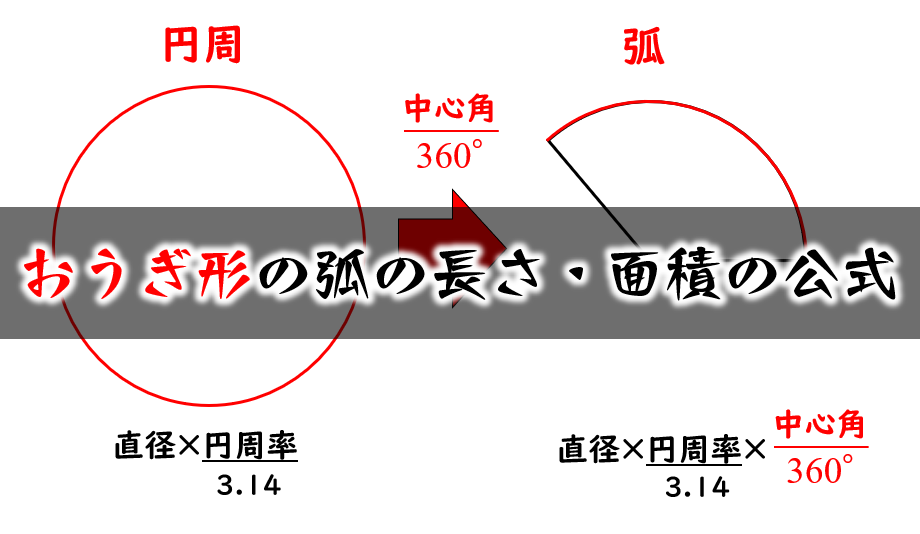
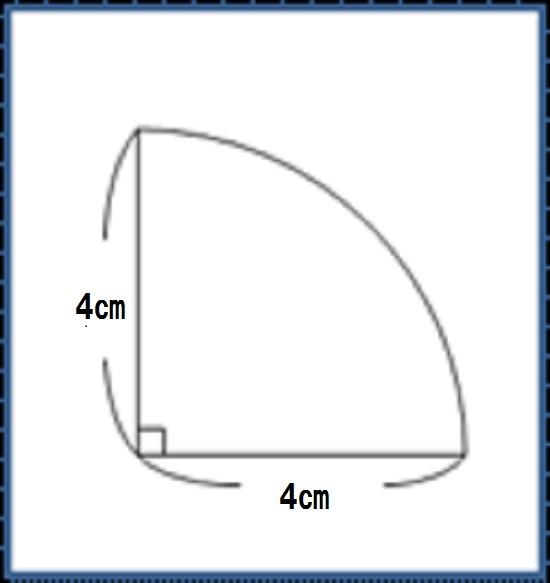
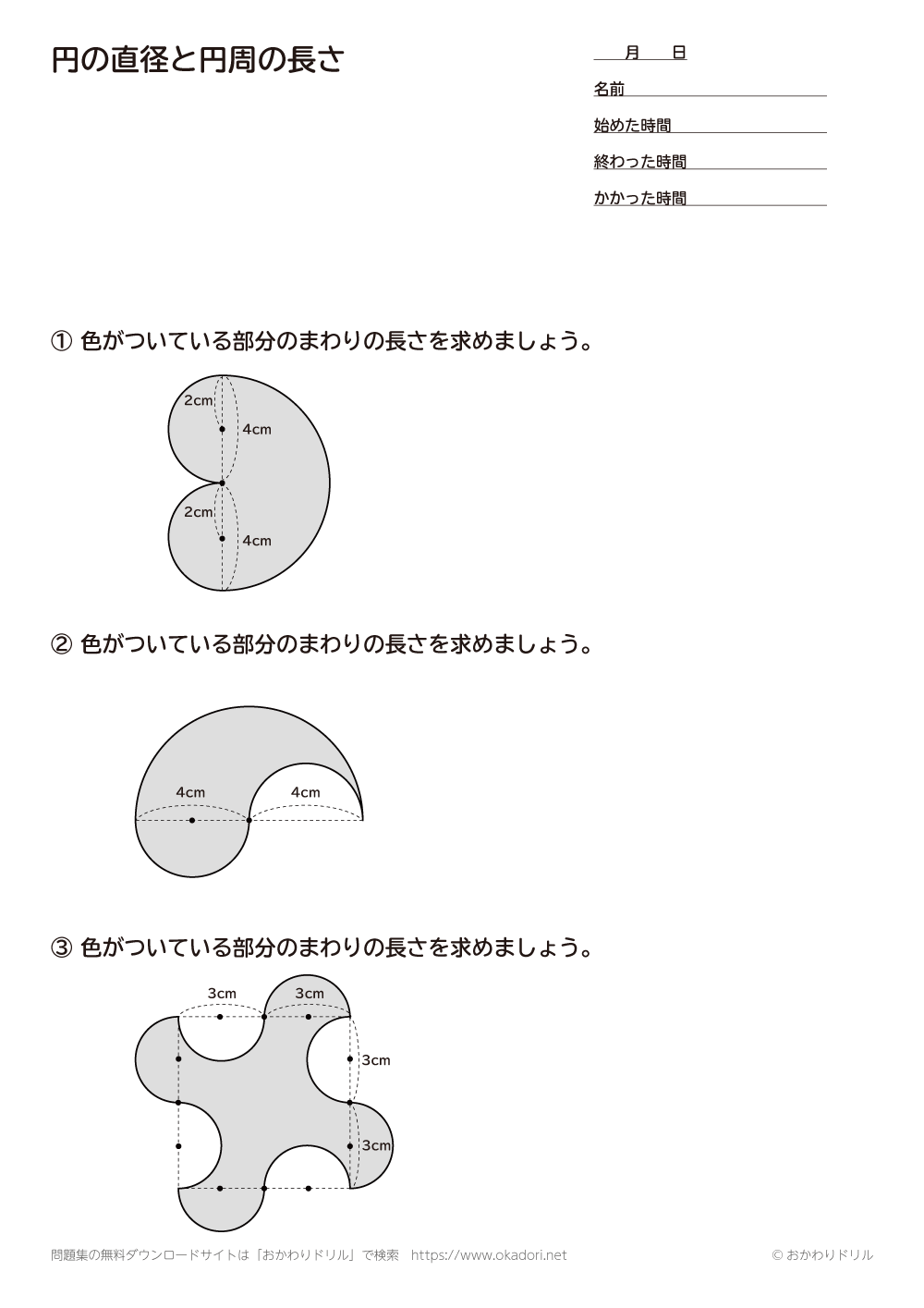
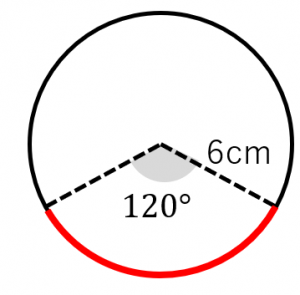
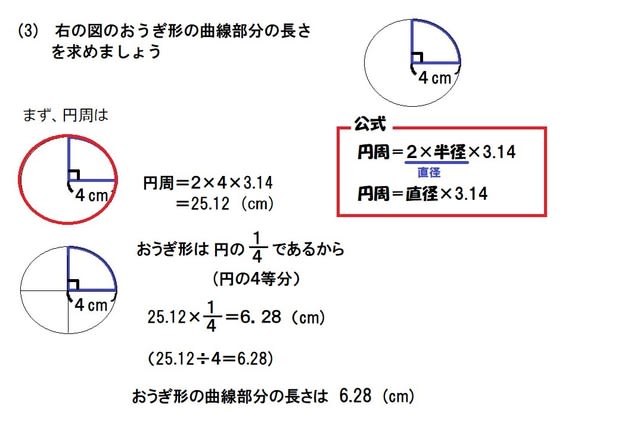
円周の長さを求める公式は 直径×3.14 (小学生向け) 直径×π (中学生以上向け) です。小学生の子は「直径×3.14」を、中学生以上の子は「直径×π」を覚えてください。πは「パイ」と読みます。ちなみに3.14やπのことを「円周率」といいます。 円周率とは、円周の直径に対する比率のこ 扇形のまわりの長さを求めるときには、次の公式を使います。 扇形のまわりの長さ =直径×円周率× +半径×2 ~考え方~ 扇形のまわりの長さは、 扇形の弧の長さに半径×2を足す ことで求めることが出来ます。
円周の長さを求める公式 小学生
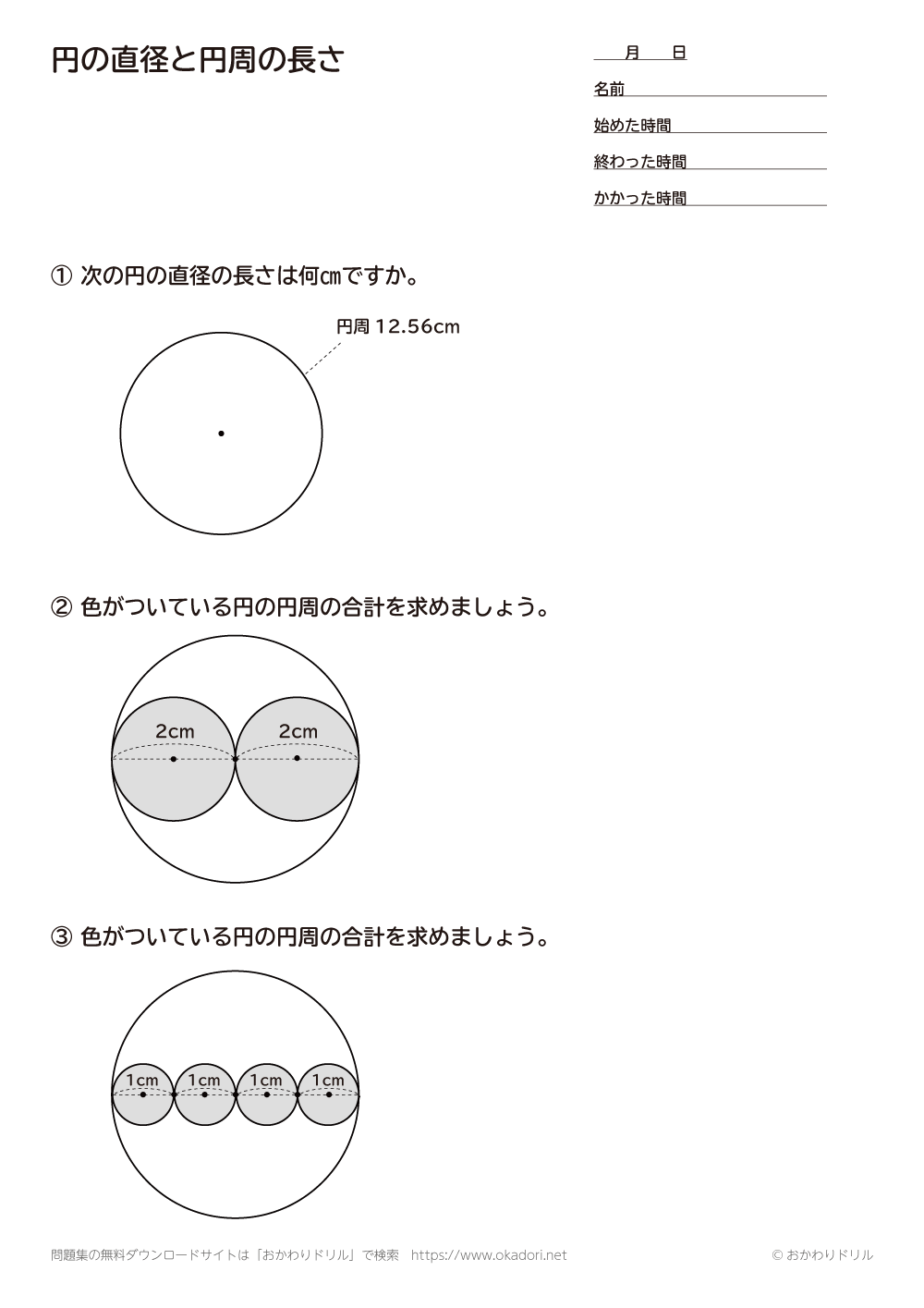
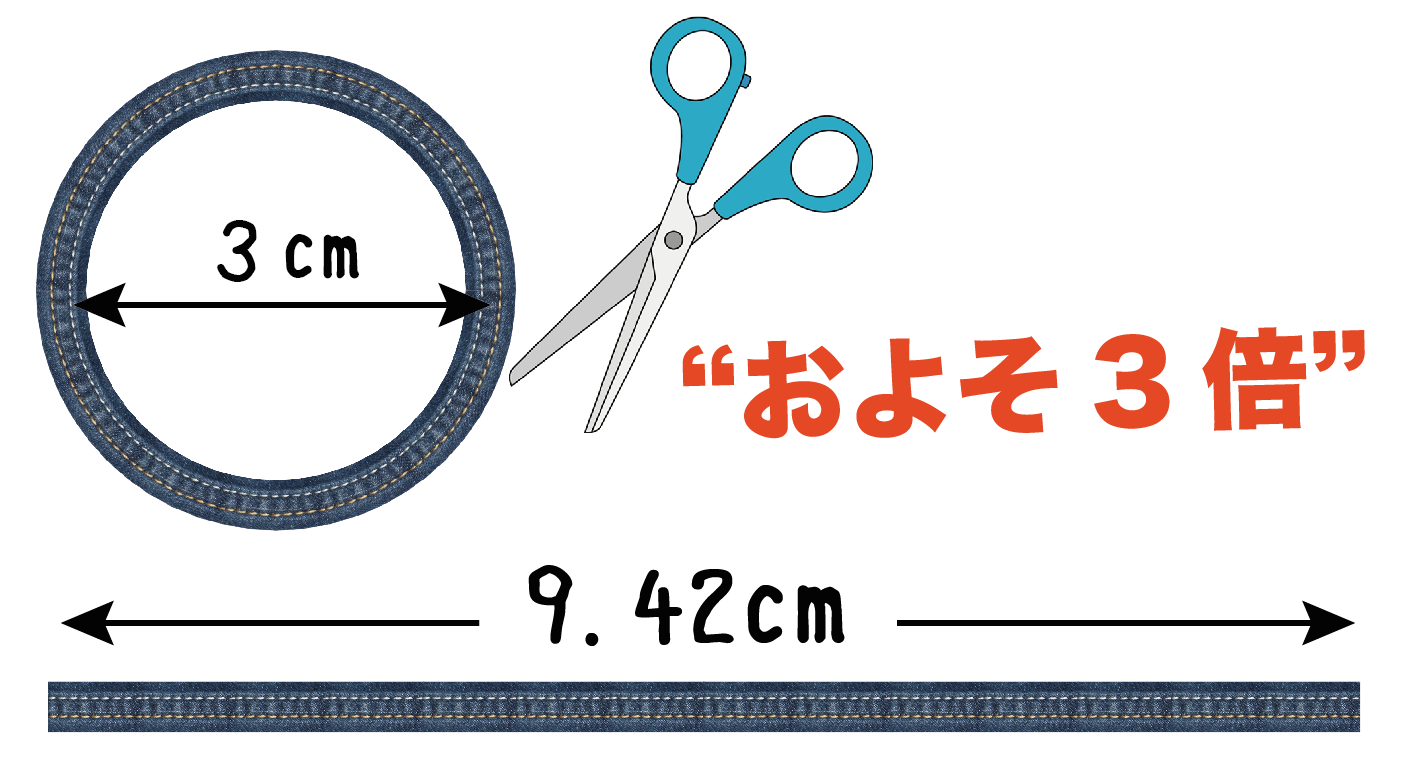
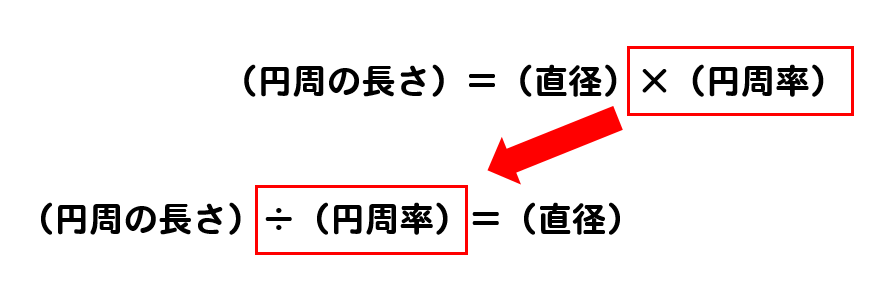
円周の長さを求める公式 小学生-円周の長さが直径の何倍になっているかを表す数を円 えん 周 しゅう 率 りつ といいます。どんな大きさの 円でも,円周率は約314です。 また,円周率を使って,直径から円周の長さを求める式を考えると,円周÷直径=円周率 だから, 円周=直径×円周率円周を求める公式は 円周 直径 円周率 円 周 = 直 径 × 円 周 率 なので、 円周 円 周 = 4 × 314 = 1256 ( c m) になります。
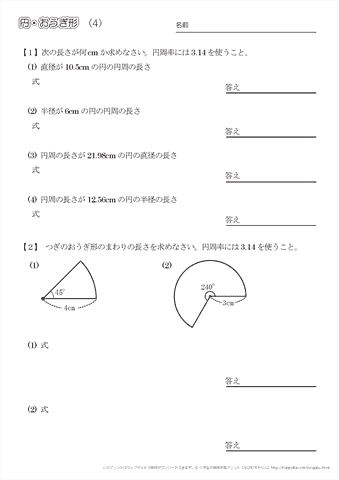
小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生
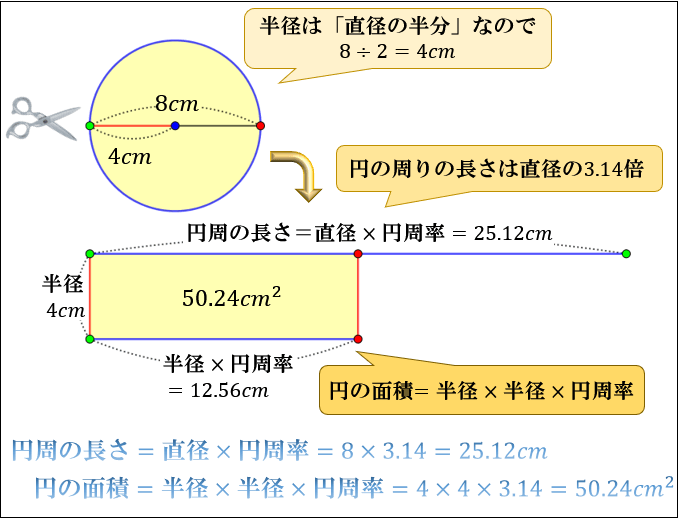
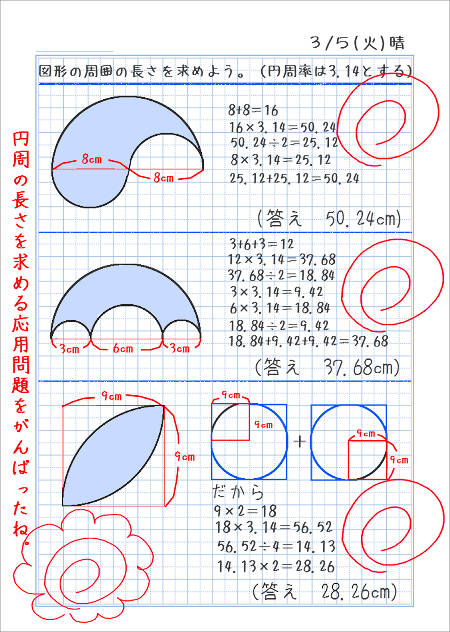
これは、楕円の円周を求めるプログラムです。 その点と点とを結んだ線の長さの総和を求める・・・というものです。 要するに、多角形により、楕円の円周の近似値を得るということです。 詳しくは、下記リンクをご参照のこと。 精度としては、長 公式に当てはめると 円周の長さ 直径 円周率 円 周 の 長 さ = 直 径 × 円 周 率 = 8 × 314 = 2512 c m 半径 直径 半 径 = 直 径 ÷ 2 = 8 ÷ 2 = 4 c m 円の面積 半径 半径 円周率 円 の 面 積 = 半 径 × 半 径 × 円 周 率 = 4 × 4 × 314 = 5024 c m 2 と求まります。 問②面積が c m 2 の円の円周の長さを求めてください。 (円周率は 314 ) 円の面積の公式から半径を円周率 πを使う = 円周 cm2 mm;
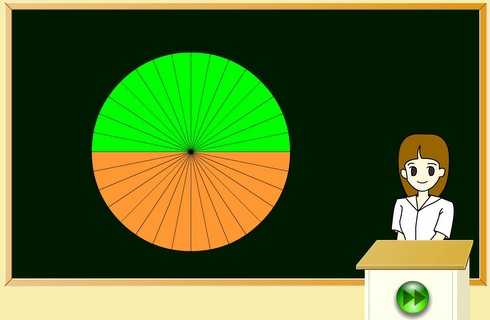
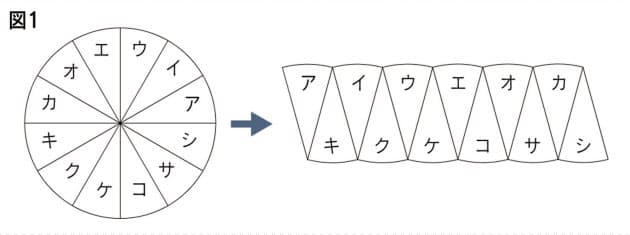
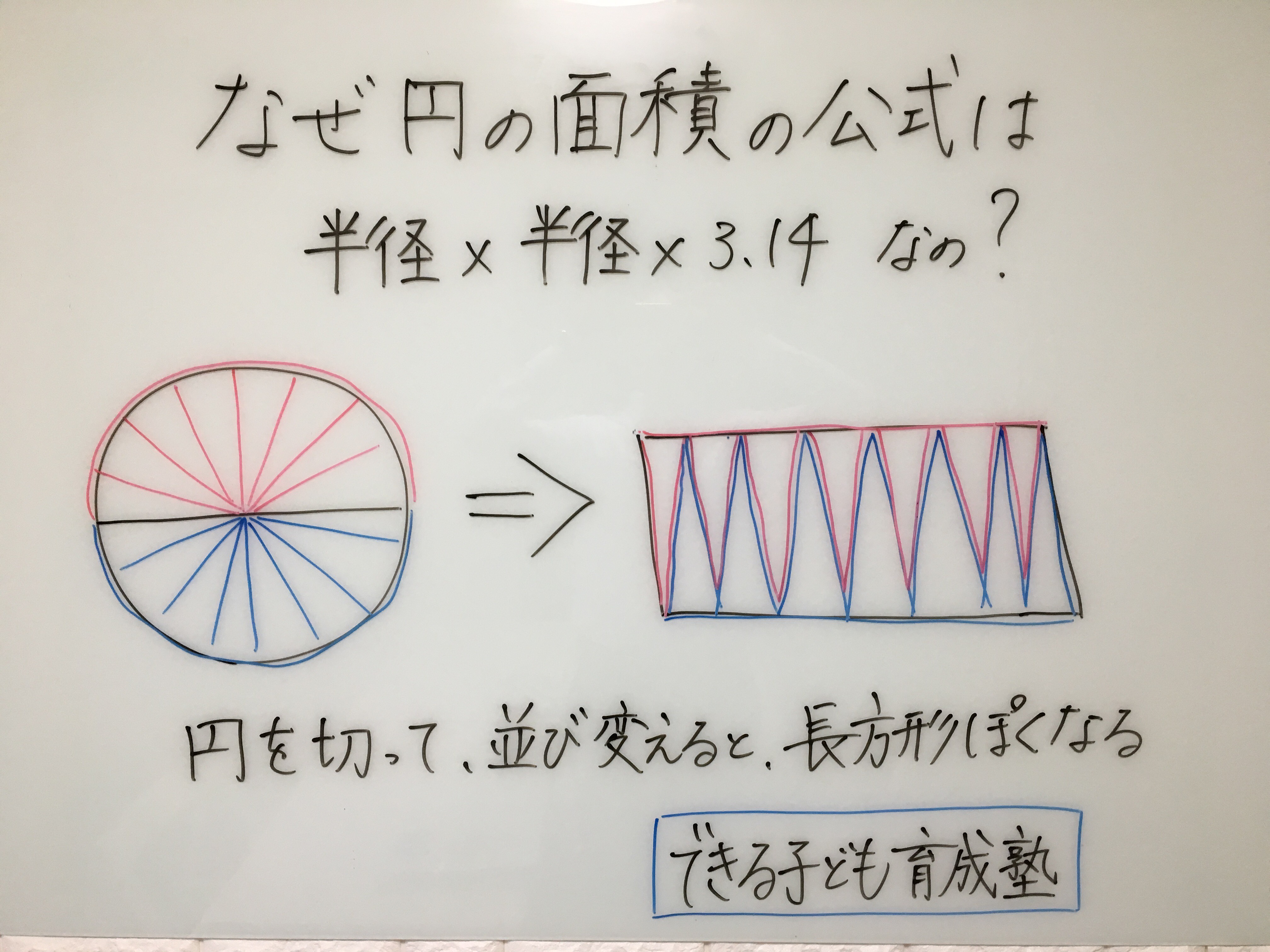
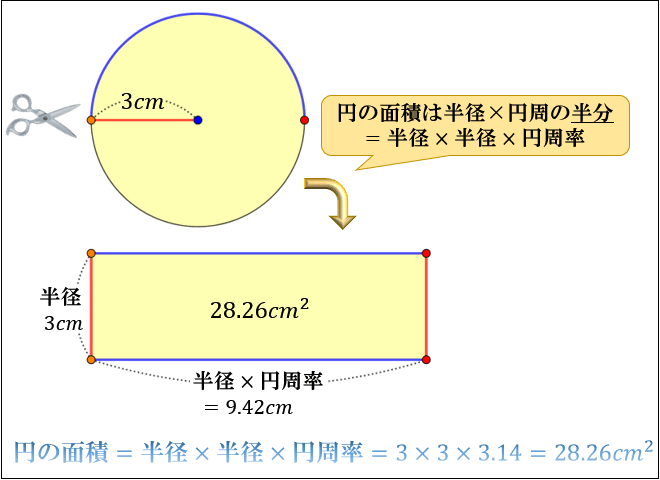
円の面積 円の面積 は、 半径×半径×314 で求めることができます。 なお、314のことを円周率といい、πと表すことも多いです。 円を細かくおうぎ形に切って、交互に逆さまに並べていくと長方形になります 。 辺の長さは、短い方が円の半径、長い方はメニュー 『円周の長さ』の電卓 URLコピー この電卓は 3万3103回 使われています 直径 cm mm;その長さが円の半径1以下であれば扇型の中に打たれた点と判断することができます。 上のことを踏まえて作成したのが次のプログラムです。 回数によって円周率の精度と処理時間を確認したいため、1000, , , , と点の数を変えて円周率を
円周の長さを求める公式 小学生のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「円周の長さを求める公式 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
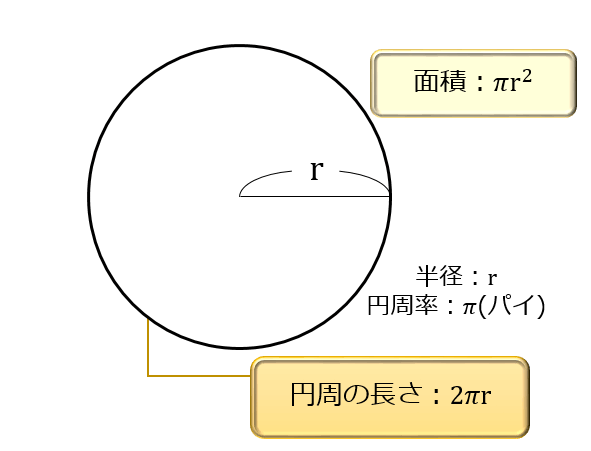 |  |
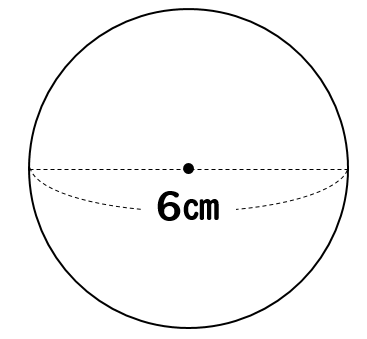
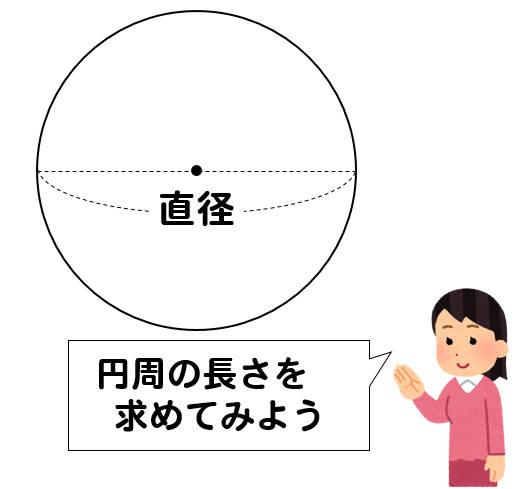
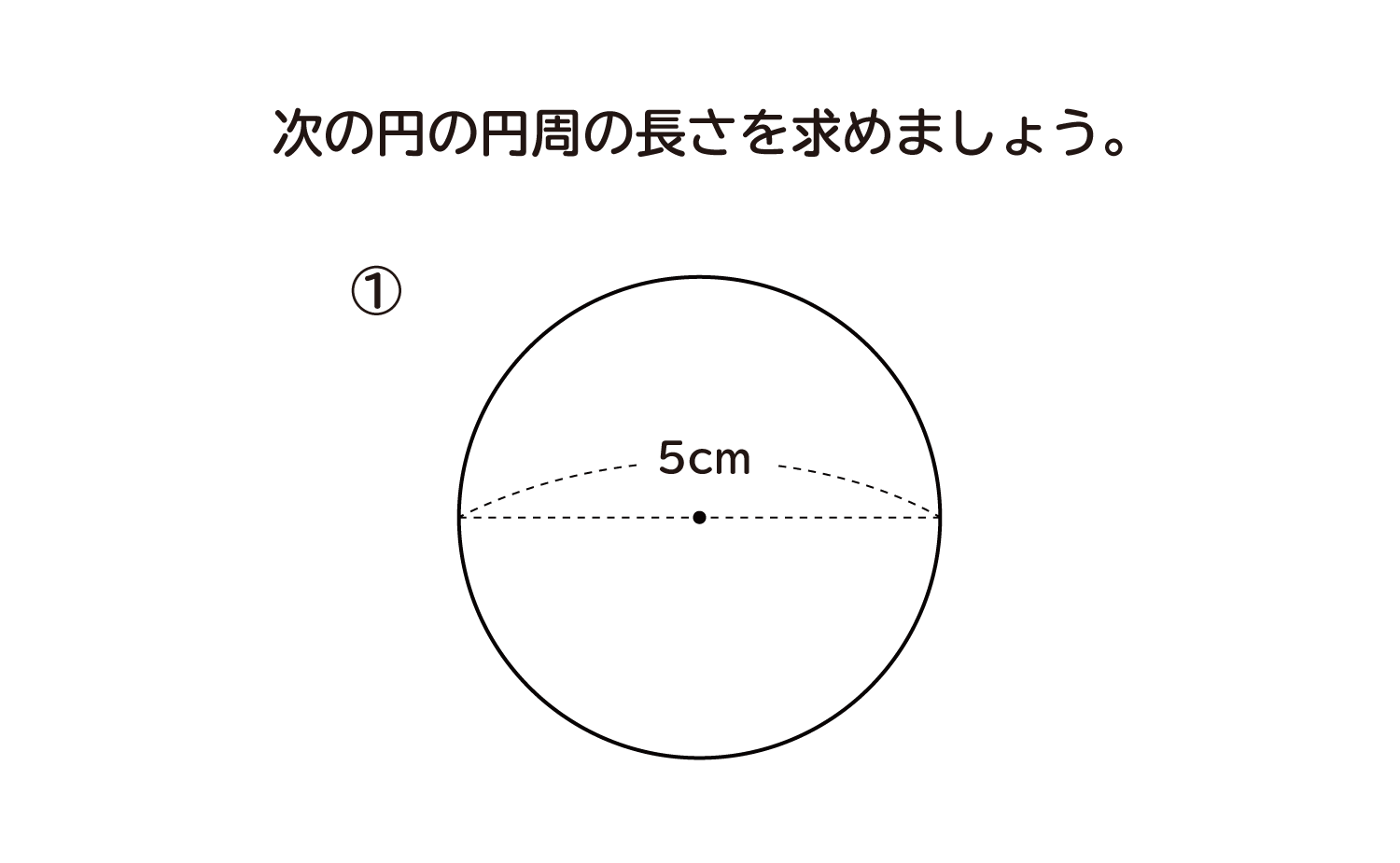
小学5年生で習う円周率と、円周の問題の解き方を、世界一やさしく解説します。 今から学ぶこと 1、 円周率 円周 (円の周りの長さ)は 直径 の約 314倍 であり、この314のことを 円周率 という 2、 円周の長さを求める式 円周 = 直径 × 314 3、 円周の一部の長さを求める問題 そして、3.14やπのことを「円周率」といいます。なので、円の面積の公式は「半径×半径×円周率」ともいえます。 小学生の子向けの問題 ・下の円について、 半径の意味は大丈夫でしょうか?半径は直径の半分になる長さのことです。図1ならAの部分
コメント
コメントを投稿